3. Fonction égale à sa dérivée : unicité

Supposons qu’il existe une fonction égale à sa dérivée et dont l’image, en 0, est égale à 1. C’est-à-dire une fonction f définie sur R et satisfaisant aux conditions du problème (P) :

 f(0) = 1 ;
 f ’(x) = f(x) pour tout réel x.

Jamais nulle

1. Calculer la dérivée de la fonction x ↦ f(-x).
2. Calculer la dérivée de la fonction x ↦ f(-x) × f(x). En déduire que cette fonction est constante.
3. Prouver que, pour tout x ∈ R, f(x)≠0.

Unicité

(Exemple de démonstration par l’absurde.)

Supposons que deux fonctions vérifient le problème (P), notons-les g₁ et g₂. D’après ce qui précède, ces fonctions ne s’annulent jamais On peut donc définir, sur R, la fonction c par :

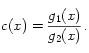
1. Justifier que c est dérivable sur R. Calculer sa dérivée. Que peut-on en déduire ?
2. Calculer c(0).
3. Que peut-on en déduire pour g₁ et g₂ ?